
下載app免費領取會員


計算三維曲線的長度是數學中的一個重要問題。三維曲線的長度是指曲線上各點之間的距離總和。在計算三維曲線長度時,我們可以利用微積分中的曲線積分來解決。
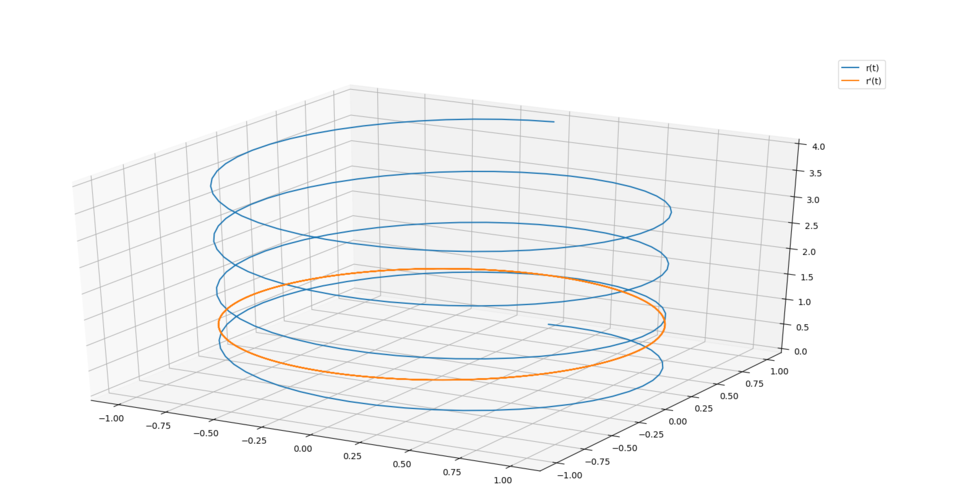
首先,我們需要將三維曲線參數化。參數化是指通過一個或多個參數來表示曲線上的點。常見的參數化方法有向量值函數和參數方程。
對于向量值函數表示的曲線,我們可以將曲線定義為一個向量函數r(t),其中t是參數。例如,我們可以將曲線表示為r(t) = (x(t), y(t), z(t))。然后,我們可以將曲線長度的計算問題轉化為對r(t)的積分問題。
對于參數方程表示的曲線,我們可以將曲線定義為三個關于參數t的函數x(t),y(t)和z(t)。然后,我們可以將曲線長度的計算問題轉化為對x(t),y(t)和z(t)的積分問題。
對于向量值函數的曲線,我們可以使用以下公式來計算曲線的長度:
L = ∫ab ||r'(t)|| dt
其中,L是曲線的長度,r'(t)是r(t)的導數,||r'(t)||是向量r'(t)的模,a和b是參數的起始值和結束值。
對于參數方程的曲線,我們可以使用以下公式來計算曲線的長度:
L = ∫ab √[(x'(t))2 + (y'(t))2 + (z'(t))2] dt
其中,L是曲線的長度,x'(t),y'(t)和z'(t)分別是x(t),y(t)和z(t)的導數,a和b是參數的起始值和結束值。
通過對曲線參數化并應用上述公式,我們可以計算出三維曲線的長度。這對于很多應用領域都非常重要,例如計算機圖形學、物理學和工程學等。
總之,計算三維曲線的長度是一個重要的數學問題。我們可以通過將曲線參數化并應用曲線積分的方法來解決這個問題。通過計算曲線長度,我們可以在各種應用領域中更好地理解和分析曲線的性質和行為。
本文版權歸腿腿教學網及原創作者所有,未經授權,謝絕轉載。

下一篇:Dynamo教程 | 三維曲線圖






推薦專題














































