
下載app免費領取會員


繪制三維曲線是計算機圖形學中的一個重要任務,它可以幫助我們可視化復雜的曲線形狀。在本文中,我們將介紹幾種常用的方法來繪制三維曲線。
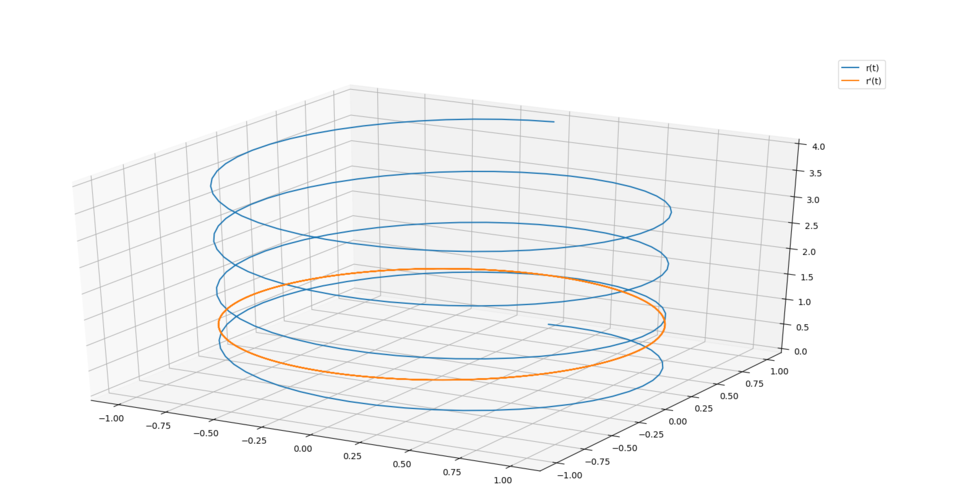
1. 參數方程法
參數方程法是最常用的繪制三維曲線的方法之一。它將三維曲線的坐標表示為參數的函數。例如,給定參數t,我們可以使用以下參數方程來表示一條三維曲線:
x = f(t), y = g(t), z = h(t)
在參數方程法中,我們可以選擇不同的函數f(t),g(t)和h(t)來得到不同的曲線形狀。常見的參數方程包括圓柱曲線、拋物線、螺旋曲線等。
2. 點集插值法
點集插值法是一種通過給定的點集來逼近三維曲線的方法。該方法通常用于曲線繪制和曲面建模。在點集插值法中,我們需要先給定一組控制點,然后通過插值算法來計算中間的點。
常見的點集插值方法包括貝塞爾曲線和B樣條曲線。貝塞爾曲線通過控制點來定義曲線形狀,而B樣條曲線通過在控制點之間插入額外的點來逼近曲線形狀。
3. 參數化曲線法
參數化曲線法是一種通過在曲線上移動一個參數來繪制曲線的方法。在參數化曲線法中,我們首先需要選擇一個基本的曲線形狀(如直線或圓),然后通過變換參數來改變曲線形狀。
參數化曲線法可以用于繪制復雜的曲線形狀,如螺旋線、橢圓和心形曲線。它也常用于動畫和特效的制作中。
4. 數學函數法
數學函數法是一種直接使用數學函數來定義三維曲線形狀的方法。在數學函數法中,我們可以通過定義直角坐標系或極坐標系下的數學函數,來表示曲線上的點的坐標。
數學函數法可以用于繪制各種曲線形狀,包括線性函數、冪函數、三角函數和指數函數等。
5. 曲面延拓法
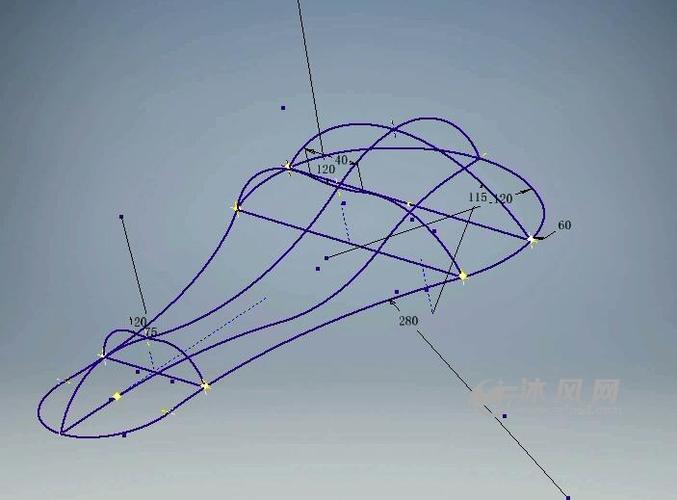
曲面延拓法是一種通過將二維曲線延拓到三維空間中來繪制三維曲線的方法。在曲面延拓法中,我們首先需要選擇一條二維曲線,然后通過在曲線的每個點上加入新的維度來將其延拓到三維空間中。
曲面延拓法可以用于繪制各種復雜的曲線形狀,如環形曲線、螺旋曲線和超橢圓曲線等。
繪制三維曲線是計算機圖形學中的一個重要任務,它可以幫助我們可視化復雜的曲線形狀。在本文中,我們介紹了幾種常用的方法來繪制三維曲線,包括參數方程法、點集插值法、參數化曲線法、數學函數法和曲面延拓法。每種方法都有其適用的場景和特點,選擇合適的方法可以幫助我們更好地繪制出所需的曲線形狀。
本文版權歸腿腿教學網及原創作者所有,未經授權,謝絕轉載。

下一篇:Dynamo教程 | 使用QwtPlot3D來繪制三維軌跡曲線






推薦專題













































