
下載app免費領取會員


繪制三維曲線是計算機圖形學中的一個重要技術,它可以幫助人們更直觀地理解和分析各種復雜的數據模型。三維曲線的繪制涉及到數學和計算機圖形學的知識,需要使用相應的算法和工具來實現。
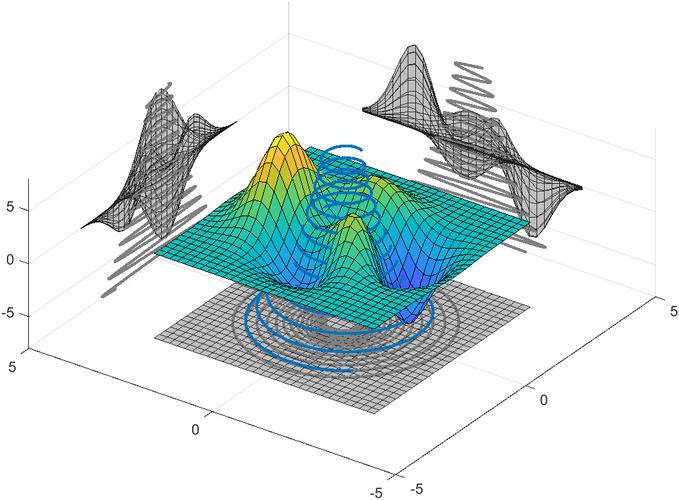
在繪制三維曲線之前,首先需要確定曲線的方程或參數化表達式。曲線方程可以是直接給定的函數,也可以是通過參數化變量得到的。在計算機圖形學中,通常使用參數化方程來表示三維曲線,其中參數是曲線上的點在空間中的位置。
繪制三維曲線的方法有很多種,下面介紹幾種常用的方法。
一種常見的方法是使用繪圖軟件或編程語言中的繪圖函數來繪制曲線。這種方法通常適用于簡單的曲線,可以通過直接輸入曲線的參數化方程或坐標點來實現。繪圖函數會根據提供的參數計算曲線上的點的位置,并將其連接起來形成曲線。
另一種方法是使用三維建模軟件來繪制曲線。這種方法適用于復雜的曲線,可以通過在三維建模軟件中創建曲線對象并設置其屬性來實現。用戶可以通過拖動控制點或調整曲線的控制參數來改變曲線的形狀和位置。
除了以上方法,還有一些更高級的技術可以用于繪制三維曲線。例如,貝塞爾曲線是一種常用的曲線繪制方法,它可以通過控制點和權重來定義曲線的形狀。貝塞爾曲線可以通過調整控制點和權重來實現曲線的彎曲和扭曲。
另外,參數曲線和樣條曲線也是常用的三維曲線繪制方法。參數曲線是通過參數化方程來定義的,可以通過調整參數值來改變曲線的形狀。樣條曲線則是通過一系列控制點來定義的,可以通過調整控制點的位置和權重來實現曲線的變形。
無論采用哪種方法,繪制三維曲線都需要處理大量的數學計算和圖形運算。計算機圖形學中有許多優化算法和技術可以用于提高繪制效率和質量。例如,曲線的渲染可以使用光線追蹤算法來實現更真實的效果,或者使用曲面細分算法來增加曲線的細節。
繪制三維曲線不僅僅是一種技術手段,它也是一種藝術表達的方式。通過合理運用顏色、材質和光照等技術手段,可以使得曲線更加生動、立體和美觀。在繪制三維曲線時,藝術性和創意同樣重要,可以根據需求和目的來選擇不同的繪制方法和風格。
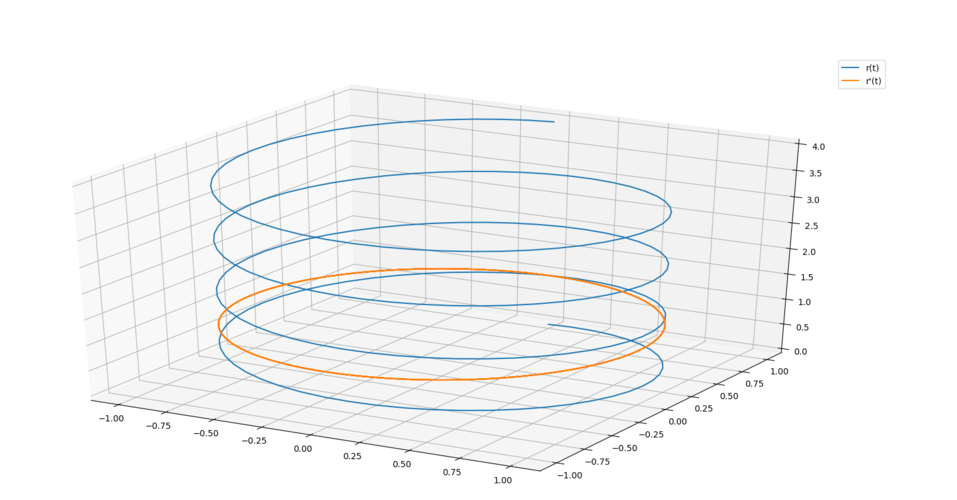
總之,繪制三維曲線是一個復雜而有趣的領域,需要掌握數學、計算機圖形學和藝術等多個領域的知識。通過不斷學習和實踐,我們可以掌握各種繪制方法和技術,進一步拓展和深化對三維曲線的理解和應用。繪制出真實、細致和美觀的三維曲線,將為我們帶來更好的視覺體驗和認知體驗。
本文版權歸腿腿教學網及原創作者所有,未經授權,謝絕轉載。







推薦專題














































