
下載app免費領取會員


三維曲線方程的描述是數學中研究曲線在三維空間中的表示和性質的一個重要課題。三維曲線可以描述空間中的各種形狀,包括直線、曲線、螺旋線等。為了描述這些曲線,數學家發展了一種基于參數方程的方法,通過引入參數來描述曲線上的每一個點的位置。

三維曲線可以用參數方程表示為:
x = f(t)
y = g(t)
z = h(t)
其中t是參數,f(t),g(t),h(t)是關于t的函數。這三個函數決定了曲線在三維空間中的形狀。通過選擇不同的函數,我們可以得到各種不同類型的曲線。
一種常見的三維曲線是直線。直線可以用參數方程表示為:
x = a + bt
y = c + dt
z = e + ft
其中a,b,c,d,e,f是常數,代表直線在三維空間中的位置和方向。通過調整這些常數,我們可以得到不同位置和方向的直線。
除了直線,還有許多其他類型的三維曲線。例如,圓弧可以用參數方程表示為:
x = rcos(t)
y = rsin(t)
z = h(t)
其中r是半徑,t是參數,h(t)是關于t的函數。這個參數方程描述了一個在平面上旋轉的圓弧。
另一個有趣的例子是螺旋線。螺旋線可以用參數方程表示為:
x = rcos(t)
y = rsin(t)
z = ht
其中r是螺旋線的半徑,h是螺旋線沿著z軸方向的變化速率,t是參數。這個參數方程描述了一個沿著z軸螺旋上升的曲線。
三維曲線的參數方程可以用來描述曲線的形狀、方向和大小。通過改變參數方程中的參數,我們可以對三維曲線進行變換。例如,改變參數的范圍可以改變曲線的長度。調整參數方程中的參數可以改變曲線的形狀,使其變得更彎曲或更直。通過變換參數方程中的常數,我們可以將曲線平移或旋轉到不同的位置和方向。
通過研究三維曲線的參數方程,我們可以深入了解曲線的性質和行為。我們可以計算曲線的切線和法線,研究曲線在不同點的斜率和曲率。我們還可以計算曲線的長度和弧長,研究曲線的彎曲程度。這些性質對于理解和應用三維曲線都非常重要。
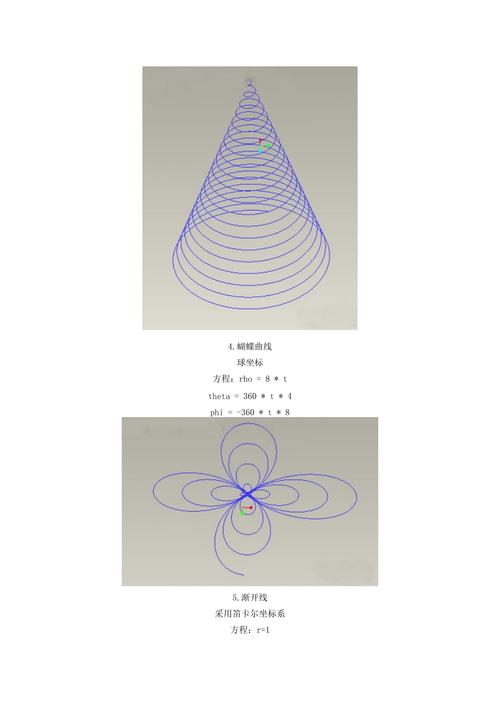
總之,三維曲線方程的描述是數學中研究曲線在三維空間中的表示和性質的一個重要課題。通過參數方程,我們可以描述和變換各種不同類型的曲線。研究三維曲線的參數方程可以揭示曲線的性質和行為,為數學研究和實際應用提供了重要的工具和方法。
本文版權歸腿腿教學網及原創作者所有,未經授權,謝絕轉載。







推薦專題














































