
下載app免費領取會員


三維曲線方程是數學中的一個重要概念,給出了描述三維空間中曲線的方法。通過三維曲線方程,我們可以準確地描述曲線在三維空間中的位置和形狀。下面我們來詳細解釋三維曲線方程。

在三維空間中,一個曲線可以由參數方程來表示。參數方程由參數t和三個關于t的函數x(t)、y(t)和z(t)組成。這些函數定義了曲線上每一點在三維空間中的坐標。
三維曲線方程的一般形式可以寫為:
x = f(t)
y = g(t)
z = h(t)
其中f(t)、g(t)和h(t)是關于參數t的函數。通過給定參數t的取值范圍,我們可以確定曲線上的點。
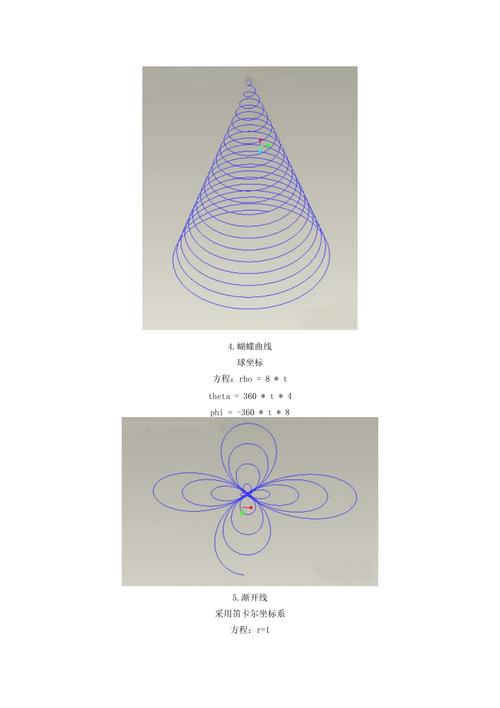
舉個例子來說明三維曲線方程的應用。假設我們有一個螺旋線,可以通過以下參數方程來描述:
x = cos(t)
y = sin(t)
z = t
這個曲線在三維空間中呈螺旋狀,x和y的值隨著參數t的變化而變化,而z的值是參數t的線性變化。通過不同的參數t取值,我們可以得到曲線上的不同點,從而描繪出整個螺旋線。
三維曲線方程的解析幾何意義是描述曲線在空間中的位置。通過解析幾何的方法,我們可以求解曲線與平面的交點、曲線的切線和法線等。這些幾何性質對于研究曲線的性質和應用都非常重要。
在實際應用中,三維曲線方程被廣泛地應用于物理、工程等領域。例如,在計算機圖形學中,三維曲線方程被用于描述和繪制曲線和曲面。在機械工程中,三維曲線方程被用于描述物體的軌跡和運動路徑。在物理學中,三維曲線方程被用于描述粒子在空間中的運動軌跡。
總之,三維曲線方程是數學中一個重要的概念,用于描述和分析三維空間中的曲線。通過參數方程的形式,我們可以準確地描述曲線在空間中的位置和形狀。三維曲線方程在物理、工程和計算機圖形學等領域有著廣泛的應用,并且為我們理解空間曲線的性質和應用提供了重要的工具。
本文版權歸腿腿教學網及原創作者所有,未經授權,謝絕轉載。






推薦專題














































